【競プロ精進ログ】ABC168-C

zuka

ABCをコツコツ解いていきます。

本記事は，管理人の競技プロ精進日記としてログを取ったものです。モチベーションを爆上げするために，積極的にアウトプットしていく作戦です。

これから競技プログラミングを始めようと考えている人や，なんとなく敷居が高いと感じている人の参考になれば嬉しく思います。その他の記事は以下をご覧ください。

本記事の概要

Atcoderで初心者用のコンテストとして開催されているAtcoder Beginner Contest（通称ABC）を解いていくものです。今回はABC168-C「: (Colon)」です。

ポイント

数学的な考察を必要とする問題です。余弦定理を利用しますが，パッと思いつける人は少ないのではないでしょうか。時針と分針のそれぞれの座標を求めてから三角関数などを使って斜辺の長さを求めるという方針でもいけないことはないですが，少し面倒です。結局，座標に持ち込むと面倒なことが起きるので，単純に幾何問題として解く方針が今回は良さそうです。

三角形の幾何問題において，2辺の長さとその間の角度から残りの1辺の長さを求めるためには，余弦定理を利用します。できれば，「幾何問題における長さと角度」と言えば正弦定理か余弦定理と条件反射で思いつけるようにしておきたいですね。

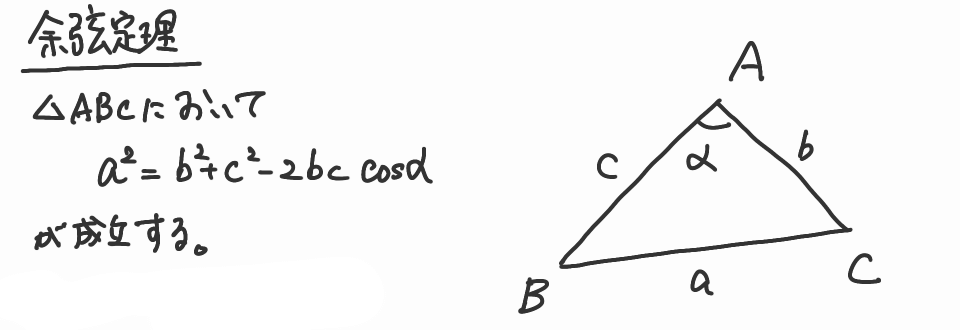
1つ注意するべきなのは，今回の問題において角度は180度を超えても大丈夫ということです。なぜなら，$\cos\theta$は$\theta$が$0 \longrightarrow \pi$と変わっていく挙動と，$\pi \longrightarrow 2\pi$と変わっていく挙動は対照的になっているからです。もう少しわかりやすく言えば，$\cos \theta = \cos(2\pi - \theta)$であり，例えば$\theta=\frac{\pi}{3}$と$\theta=2\pi - \frac{\pi}{3}$は同じになるからです。

したがって，今回の問題で三角形の角度を求めるためには，秒針と短針の動いた角度の差を考えるだけでOKです。180度より大きかった（鈍角の）場合には，わざわざ360度から引くという処理を行わなくても大丈夫です。

他にも，演算でlong doubleにキャストしないでintで計算してしまうと誤差が発生するので注意が必要です。また，時針は分針が動く$M$分の間も動き続けている点にも気をつけてください。管理人はここで引っかかりました。

実装

#include <bits/stdc++.h>
#define _GLIBCXX_DEBUG
#define rep(i, n) for (int i = 0; i < (int)(n); i++)
#define repi(i, a, b) for (int i = (int)(a); i < (int)(b); i++)
using namespace std;
typedef long long ll;

long double A, B, H, M;
long double angle;

int main(){
  cin >> A >> B >> H >> M;
  // 時針と分針が動いた角度の差
  // 時針はM分の間も動き続けていることに注意
  // 単位は[度]
  angle = (30 * H) + (30 * M / 60) - (6 * M);

  // [度]と[radian]に変換する
  long double radian;
  radian = (angle / 180) * M_PI;

  // 余弦定理の利用
  // sqrtlは平方根の結果をlong doubleで返してくれる
  // coslもcosの値をlong doubleで返してくれる
  long double ans;
  ans = sqrtl((A*A + B*B) - (2*A*B*cosl(radian)));
  cout << fixed << setprecision(20);
  cout << ans << endl;
}