 zuka
zukaABCをコツコツ解いていきます。
本記事は,管理人の競技プロ精進日記としてログを取ったものです。モチベーションを爆上げするために,積極的にアウトプットしていく作戦です。
これから競技プログラミングを始めようと考えている人や,なんとなく敷居が高いと感じている人の参考になれば嬉しく思います。その他の記事は以下をご覧ください。
本記事の概要
Atcoderで初心者用のコンテストとして開催されているAtcoder Beginner Contest(通称ABC)を解いていくものです。今回はABC117-C「Streamline」です。
ポイント
骨のある問題でした。この問題のポイントは「ゴールをシンプルにとらえる」点と「求める対象を反転させる」という点です。まずは,問題をシンプルに捉えましょう。
まず,与えられた座標の大小がごちゃごちゃになっているので,ソートして考えます。与えられた座標を$X_1,\ldots,X_M$とおけば,この問題のゴールは「$M$個の座標から$N$個の区間を選ぶ」という問題になります。
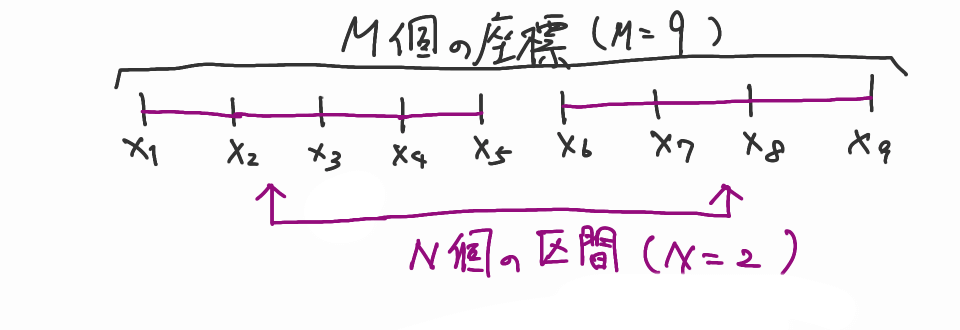
さて,次のポイントです。「求める対象を反転させ」ます。今回求める対象は「$N$個の区間」です。言い換えれば「$N$個のコマが訪れる区間」です。これを「$N$個のコマが区間の全てを訪れない区間」と反転させて考えます。
すると,$N$個のコマが区間の全てを訪れない区間を選ぶという操作は,与えられた$M$個の座標間の距離から$N-1$個を選ぶという操作になります。$M$個の座標間の距離は$M-1$個存在することに注意です。
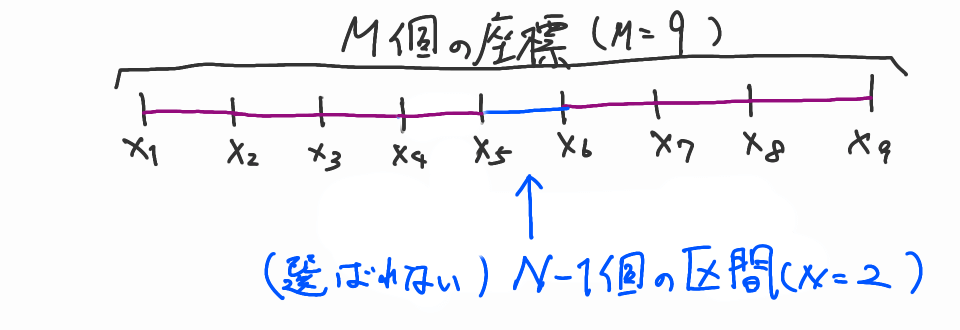
やや抽象的でわかりにくいですね。サンプルの1番目を利用して考えてみます。$N=2$,$M=5$,$X=\{1,2,10,12,14\}$です。ゴールは「$5$個の座標から$2$個の区間を選ぶ」です。実際に,答えを見てみると,区間$[1,2]$と区間$[10,14]$が選ばれていることが分かります。
ここで,求める対象を反転させてみます。つまり,2個のコマが区間の全てを訪れないような区間を考えます。このサンプルの場合は,各座標間の距離$\{1,8,2,2\}$から1つを選ぶということに相当します。実際に,答えを見てみると,$\{8\}$が選ばれていることが分かります。
なぜ区間を1つだけ選ぶのかというと,置けるコマの数が2つだからです。置けるコマの数が$N$個のとき,最後に訪れきれていない区間の個数は最大で$N-1$個になります。植木算ですね。
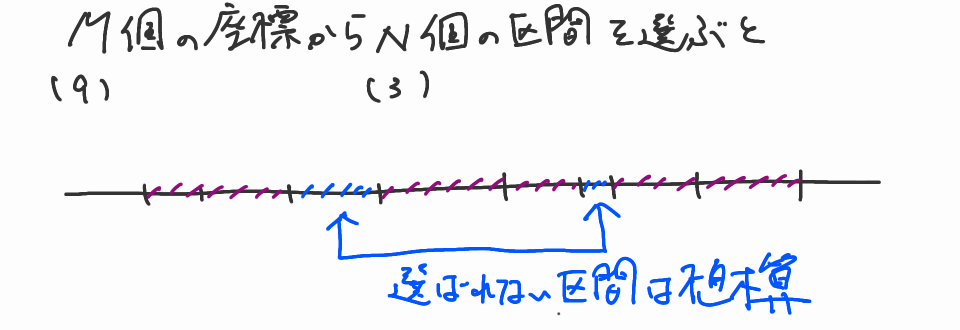
この問題の核心は,$\{8\}$の選び方にあります。この$\{8\}$は各座標間の距離$\{1,8,2,2\}$の最大値ですね。なぜなら,「コマが区間の端から端までを訪れる必要のない区間」は,出来るだけ長い方が良いですからね。
したがって,問題の答えは$M-1$存在する各座標間の距離を小さい方から$(M-1) - (N-1) = M-N$個足し合わせた数が答えになります。ただし,$M \leq N$の場合は最初にコマを置いた時点で全ての座標を訪れることができますから,答えは$0$になります。
ゴールをシンプルに捉える
求める対象を反転させる
実装
#include <bits/stdc++.h>
#define _GLIBCXX_DEBUG
#define rep(i, n) for (int i = 0; i < (int)(n); i++)
#define repi(i, a, b) for (int i = (int)(a); i < (int)(b); i++)
using namespace std;
typedef long long ll;
int N, M;
int X[100010];
int Y[100010];
int ans;
int main(){
cin >> N >> M;
rep(i, M) cin >> X[i];
// 座標をソート
sort(X, X+M);
// 座標間の距離を計算してソート
rep(i, M-1) Y[i] = abs(X[i+1] - X[i]);
sort(Y, Y+M-1);
// N <= Mの場合は最初から全ての座標にコマを置ける
if (M <= N) cout << 0 << endl;
// それ以外の場合は座標間の距離を小さい方からM-N個足し合わせたものが答え
else{
rep(i, M-N) ans += Y[i];
cout << ans << endl;
}
}

コメント